It is useful to think about what it means to multiply and divide lengths, areas, and volumes.

Here are a few questions about lengths:

• What is a length times a number?
• What is a length times a length?
• What is a length divided by a number?
• What is a length divided by a length?

Here are some questions about areas:

• What is an area times a number?
• What is an area times a length?
• What is an area divided by a number?
• What is an area divided by an area?
• What is an area divided by a length?

Here are some questions about volumes:

• What is a volume times a number?
• What is a volume divided by a number?
• What is a volume divided by a length?
• What is a volume divided by an area?
• What is a volume divided by a volume?

Unit Conversion

We often need to convert between units of area and volume. When we do this, we need to look out for some common mistakes.

Dimensions

• A length is a dimension
• Area has dimensions of length squared
• Volume has dimensions of length cubed

Units

• Any two lengths multiplied is a valid unit of area
  • meters squared
  • inch-feet
• Any three lengths multiplied is a valid unit of volume
  • meters cubed
  • inch-feet-meters
• An area times a length is also a valid unit of volume
  • acre-foot
• We have units of area that don’t use lengths
  • acre
• We also have units of volume that don’t use lengths
  • liter
  • gallon

Intuition

• What is something about the volume of a milliliter?
• What is something about a liter?
• A cubic foot?
• A cubic meter?

It is useful to have a visualization of how linear conversions, area conversions, and volume conversions are related. The Rubik’s Cube is a good visualization.

If we imagine the three-by-three cube side as a yard, we can imagine each block as a foot. Then we see that there are

• 3 feet in a yard
• 9 (3 x 3) square feet in a square yard
• 27 (3 x 3 x 3) cubic feet in a cubic yard

Roots

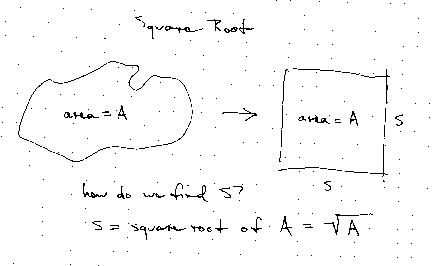
Roots answer the question, what is the size of square or cube that I can fit a given quantity in?

Square roots

• If I have a certain area, how do I find the square that contains that area?

Square Roots

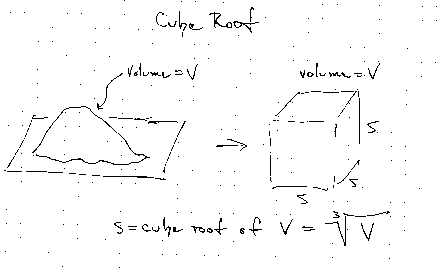
Cube roots

• If I have a volume, how do I find the cube that contains that volume?

Cube Roots

Examples of area models

GPA

The calculation of a grade point average can be thought of as an area problem.

The average is the height of a rectangle that is 10 units long, or 2.79.

Average Power

If we have a power that is changing over time, we can interpret the area under the curve as an energy. The average power is the height of a rectangle with the equal width and area.

Average Power

If we have a power that is changing over time, we can interpret the area under the curve as an energy.
The average power is the height of a rectangle with the equal width and area.

Pythagorean theorem

a^2 + b^2 = c^2

• We usually interpret as a relation between the sides of a right triangle
• We can also interpret as a statement about the areas
• It uses an equality

Pythagorean theorem

- Strogatz, The Joy of X

Pythagorean theorem

- Strogatz, The Joy of X

Pythagorean theorem

- Strogatz, The Joy of X