Linear Scales
When we are reading most graphs and maps, there is a linear, proportional relationship between the distance on the page or screen and the data.
- On a map, there is a bar showing the scale length of a mile and a kilometer.
- On a graph, there is a relationship between the length on the page and the data.
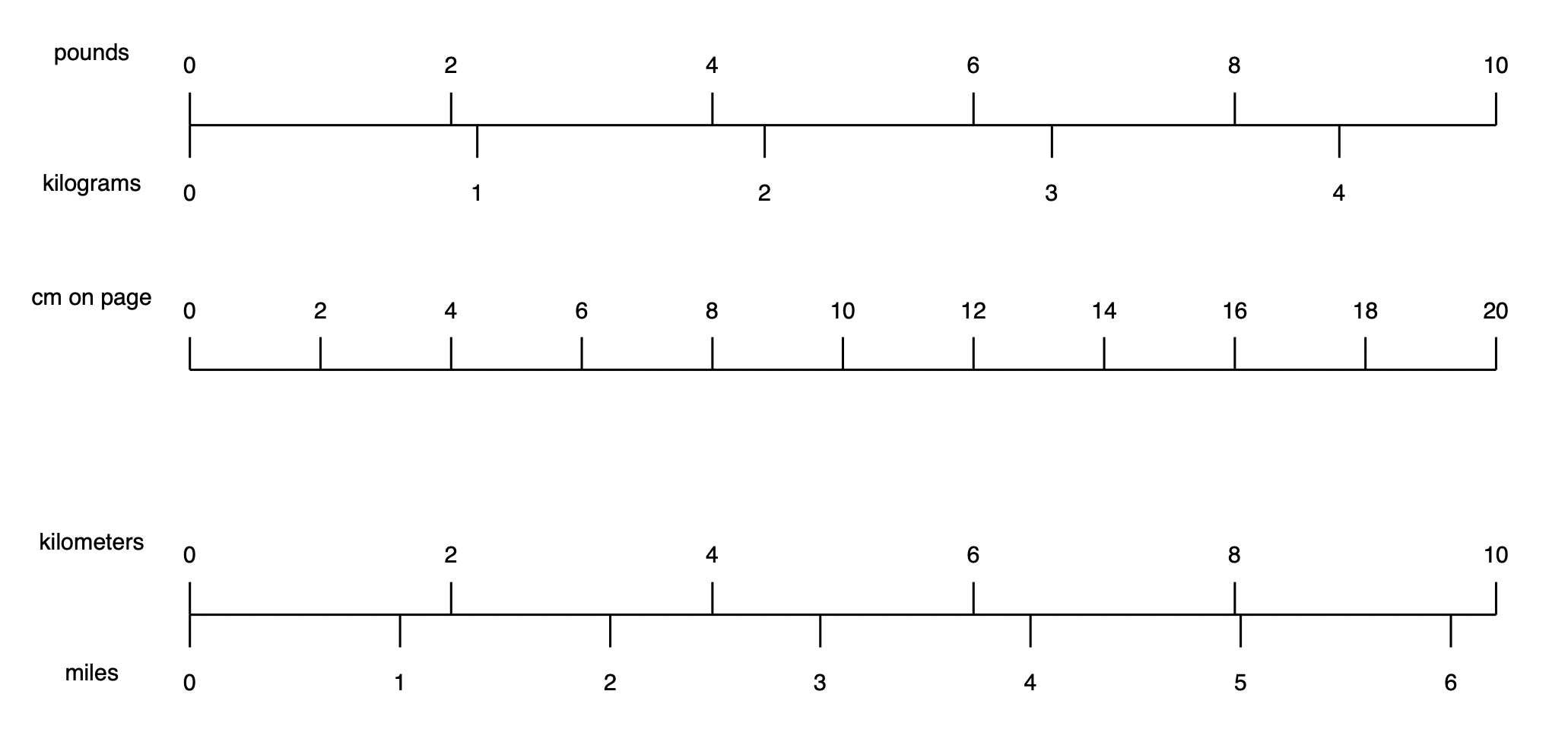
On the page, the scale is 1 pound per 2 centimeters. We can write this as \frac{1\ pound}{2 cm}. We can convert this scale ratio to the scale ratio for kilograms.
\frac{1\ pound}{2\ cm} \frac{kg}{2.2 pound} = \frac{1 kg}{4.4\ cm}
We see this is correct on the scale.
Unit Conversions and Slopes
Our eyes can interpret slopes as different when they are the same.
In both of these graphs, the slope is 2.2 pounds per kilogram, but because of the different scale (pixels to pound), they look different.
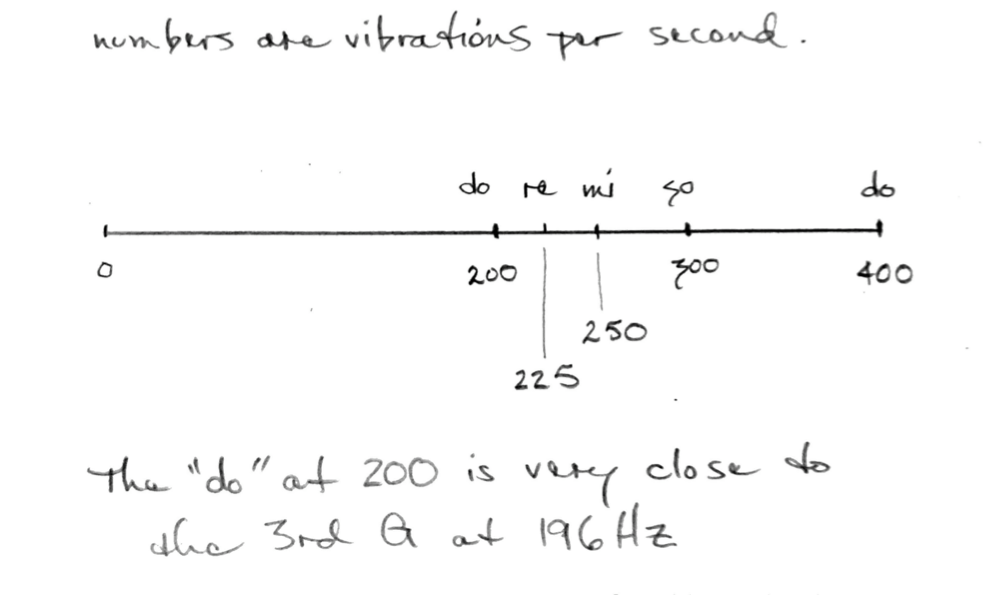
Linear Scale and Music
This is a linear scale. Note that “so” falls at the midpoint (arithmetic mean) between do and do. Also, that “mi” falls at the midpoint between do and so and that re is at the midpoint between do and mi.
Because of these mathematical relationships, these notes are pleasing to our ears.
DBH Tape
We are placing two scales on our line:
- circumference centimeter scale
- this scale directly measures the circumference
- diameter centimeter scale
- this scale “calculates” the diameter
The circumference scale is a 1-to-1 scale so
1 \textrm{ circumference scale centimeter unit} = 1 \textrm{ paper cm}
Because C = \pi d
1 \textrm{ circumference scale centimeter unit} = \pi \cdot 1 \textrm{ diameter scale unit}
We can create unit conversion factors for each of these
To determine the distance on the page between the zero and the one on the diameter centimeter scale, we convert from
- diameter centimeter scale to circumference centimeter scale
- from circumference centimeter scale to paper centimeters
1 \textrm{ dia cm scale} \cdot \frac{1 \textrm{ circ cm scale}}{\pi \cdot 1 \textrm{ dia cm scale}} \cdot \frac{1 \textrm{ paper cm}}{1 \textrm{ circ cm scale}} = 0.318 \textrm{ cm}