Place Value

This section explores our number system and how it works. Why can we represent any number between positive and negative infinity with only ten distinct symbols? The answer is that the position of each symbol relative to the other numbers changes its value.

Another question for you to think about is, why do you “carry the one” when you add and multiply?

Early number systems

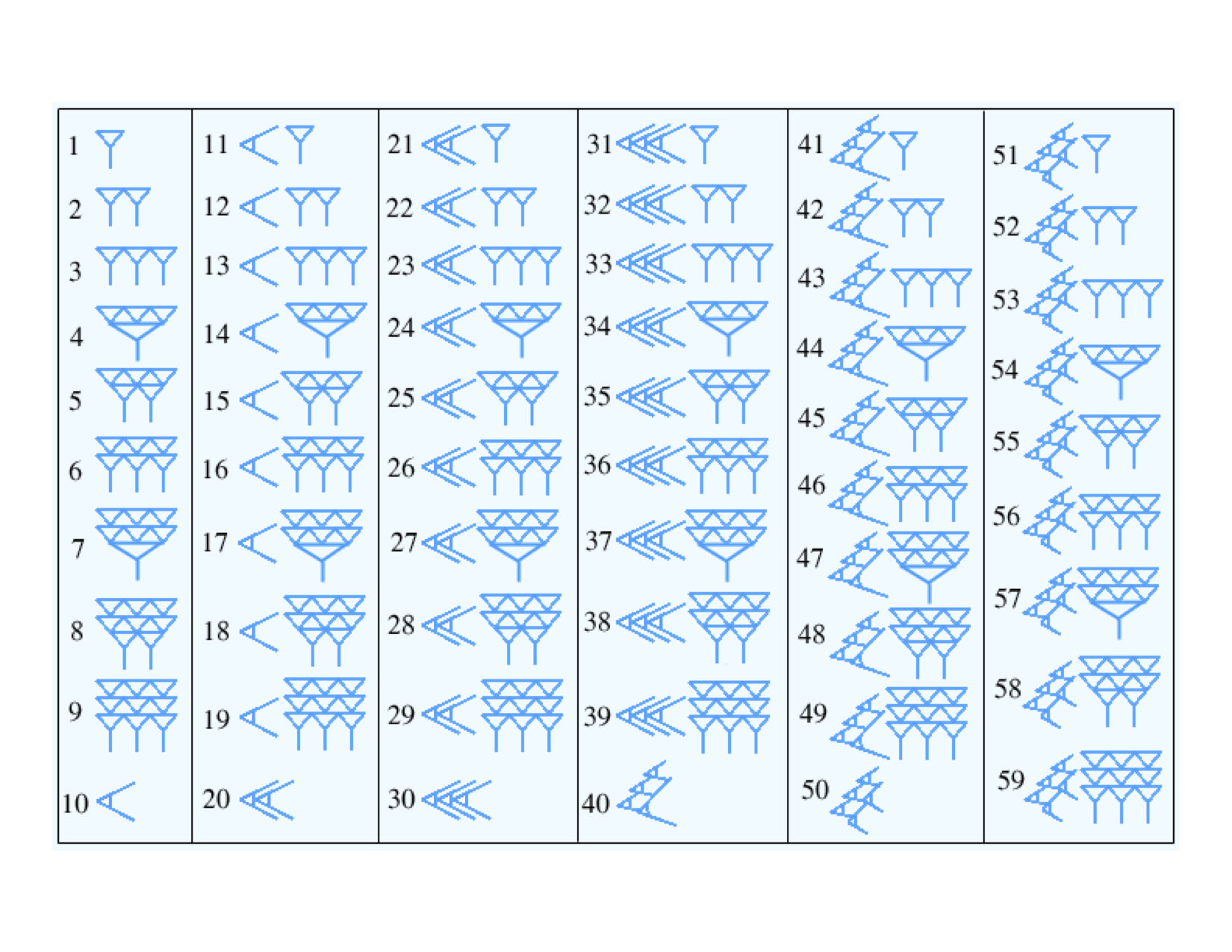
Early number systems seem reminiscent of a tally system.

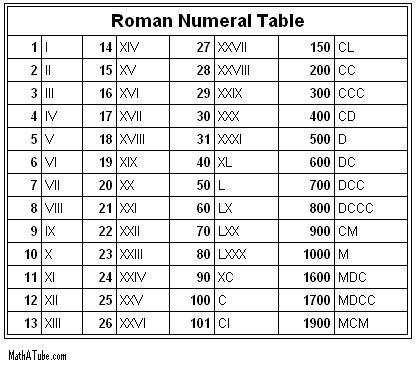
Roman numerals
Babylonian base 60

Babylonian Numerals

Roman Numerals

The invention of the zero

The invention of the zero was a significant advance in our number systems.

Modern Numbers

Base 10 Place Value Systems

The value of a digit depends on its position relative to our decimal point. Notice that although we don’t always write the decimal point, its position is always important.

Different bases

We can use any number as the basis of a place-value system
Computers use base 2 and 16
These bases provide different representations of the same number

The number 5

Here are five dots …..
We can call this “five”
Others call it “cinco”
In decimal we call it “5”
In binary we call it “101”

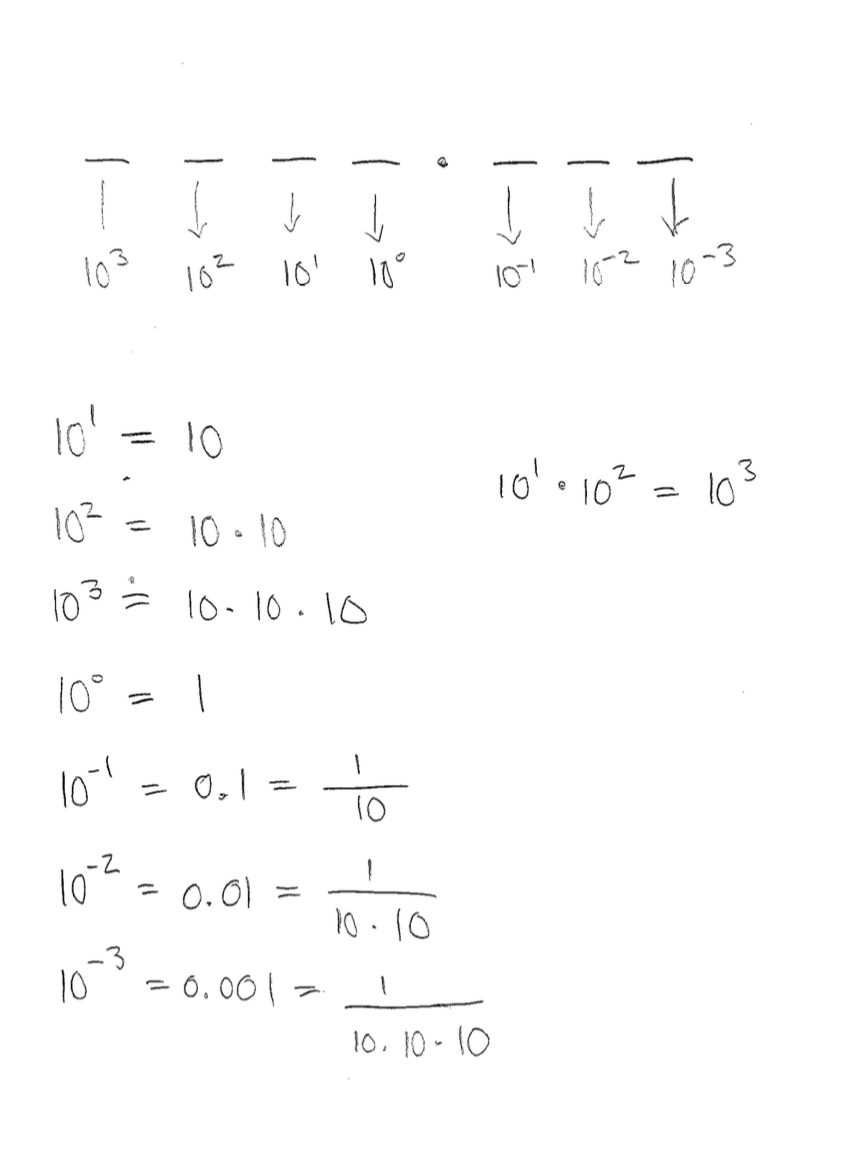
Base 10 Rules

Place to the left of the decimal is worth 1
Every place is worth 10 times the place on its right
There are only ten symbols (0 through 9)
- (Remember, 10 is not a symbol, it is a combination of 1 and 0.)
If we exceed the available values, we go to the left

Base X Rules

Place to the left of the decimal is worth 1
Every place is worth X times the place on its right
There are only X symbols (0 through X-1)
- (Remember, X is not a symbol, it is a combination of 1 and 0. First rule of base X, don’t talk about X.)
If we exceed the available values in a place, we go to the left

Counting

Base 10	Base 8	Base 5	Dots
1	1	1	.
2	2	2	:
3	3	3	:.
4	4	4	::
5	5	10	::.
6	6	11	:::
7	7	12	:::.
8	10	13	::::
9	11	14	::::.
10	12	20	:::::

Our Base 10 System

What if you only have eight fingers?

Base 8

8^0 = 1
8^1 = 8
8^2 = 64

Binary representation

A base 2 system is the basis for computer representations of numbers.

The computer performs all calculations in binary and then converts to decimal.

Hexadecimal representation

This is a base sixteen representation. It includes the letters A, B, C, D, E, and F to represent 10, 11, 12, 13, 14, and 15.

You may see this if you have worked with computer colors for websites or graphic design.

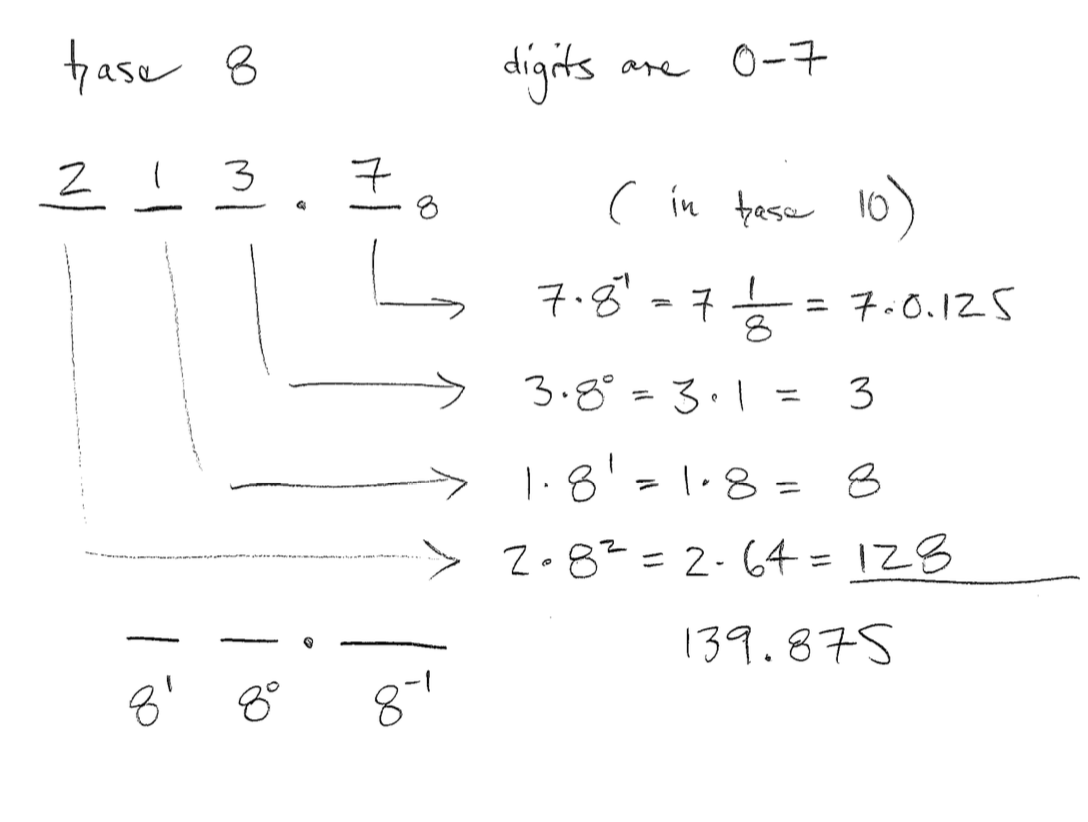
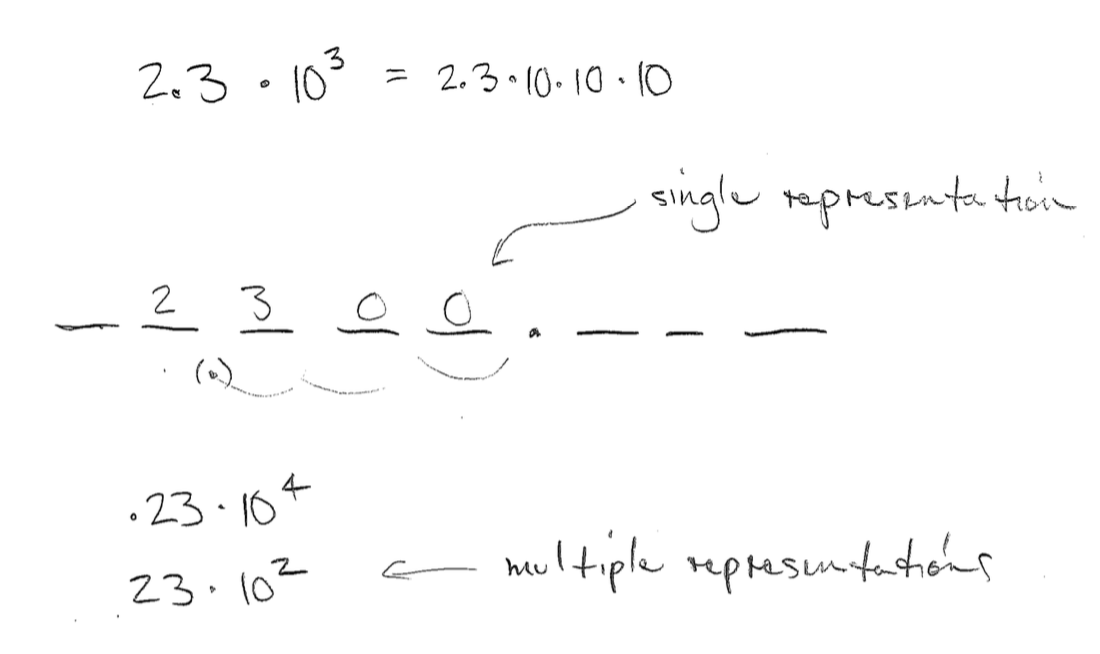
Hand Calculation Algorithms

The techniques you learned to add, subtract, multiply, and divide numbers exploit the place value system.

Imagine multiplication if you had only tally marks or stones as a representation. To multiply 5 by 6, you would make five piles of six stones and then carefully count all 30 stones to arrive at your answer. Any multiplication resulting in an impractical number of stones would be beyond your capability.

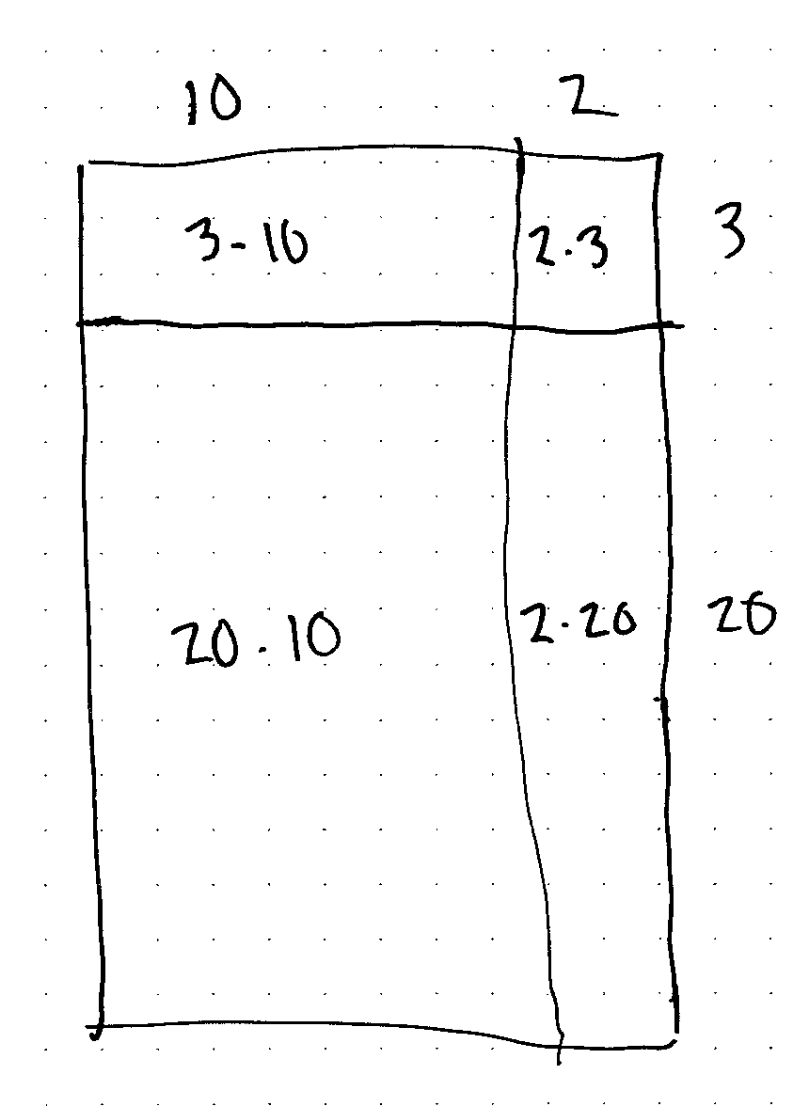
Visualization of multiplication areas

See written notes

Visualization of multiplication algorithms

Do you understand how these algorithms work?
Can you see them as a tree model estimation?

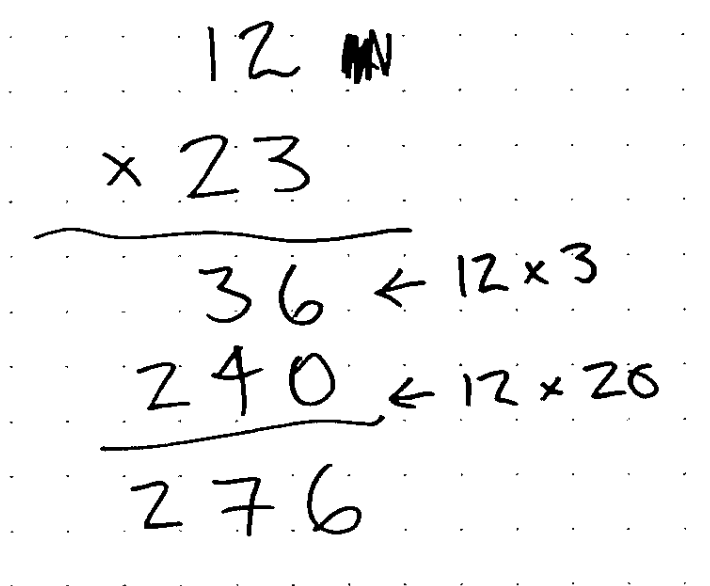
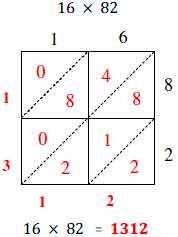
Lattice multiplication

Division

Repeated subtraction
Long division
Repeated quotients

Learning Objectives

Understand the role of place-value in our algorithms

Multiplication

Repeated addition
Place value allows for simple algorithms to compute multiplication
Traditional multiplication
Lattice multiplication