Exponential Concepts
We will look at a few related things
- logarithmic scales
- exponential functions
- exponential notation
Each of these provide tools for working with situations that exhibit exponential growth. For example, a population or bank balance is multiplied by a number each time a year goes by.
Exponential models fit these things well:
- Populations
- Contagious disease spread
- Credit card balances
- Viral videos
- Piano Keyboard
Mathematically, these functions have a fixed ratio between the y-axis values when the corresponding points on the x-axis have the same difference.
Exponential Examples
Folding paper
- Zero folds 2^0 makes one sheet thick
- One fold 2^1 is two sheets thick
- How many times can you fold?
- How can we express the number of pages by the number of folds?
- Can we write out the pattern?
\textrm{pages} = 2^{\textrm{folds}}
Rabbits
- start with two
- wait one year
- now we have double (4)
- wait another year
- now we have eight (8)
- how many in 5 years?
The number of rabbits at the start of the generation (starting with generation zero) is \textrm{rabbits} = 2^{\textrm{generations+1}}
Money grows the same way
- Start with $1000
- Grow by 10%
- Now $1100
- Grow by 10%
- Now $1210
1000 \cdot (1+0.10)^{years}
Piano Scale
Exponential Growth
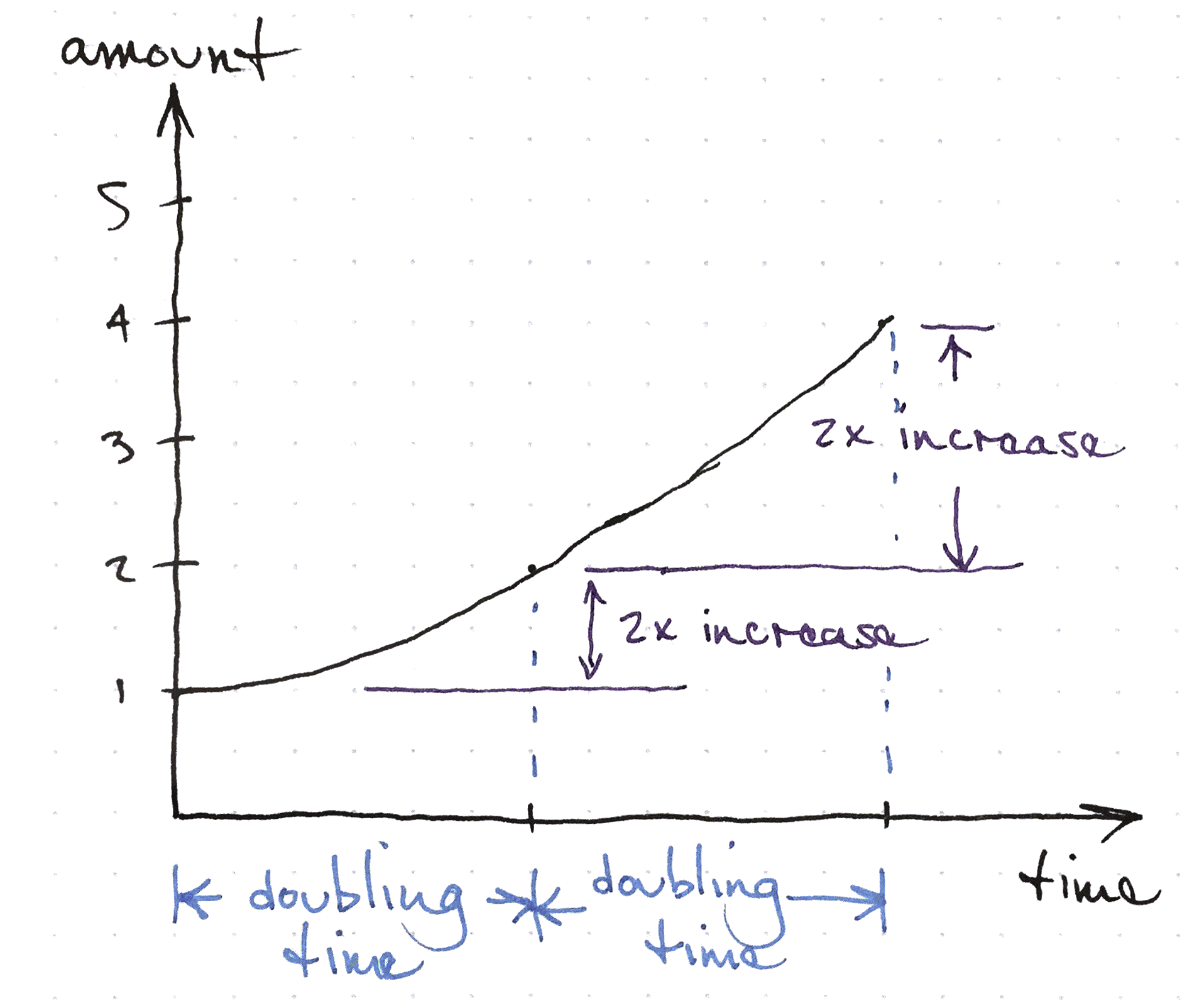
Constant Growth
This is in contrast to linear growth where if you wait for the amount to increase by a fixed amount, the amount will always increase by that fixed amount in that amount of time.
For linear growth, the slope of the function is a number that does not change along the function.

Exponential notation
You’ve probably seen notation like x^2 or x^3 several times before. In exponential notation, our symbol for a variable, x is in the exponent.
For example 2^x or 3^x.
Recall that 1 = 2^0, 2 = 2^1, 2 \cdot 2 = 2^2 = 4, etc. So, 2^x means to multiply 2 by itself x times.
Relationship Between Exponents and Logarithms
The logarithm is the inverse of an exponential function.
That is if you know that
y = 10^x
then you can take the log of both sides to solve for x.
\log_{10} y = \log_{10} 10^x = x
Note that the logarithm function has to correspond to the number being exponentiated.
When we use the number e we use the natural log \ln
y = e^x
\ln y = \ln e^x = x
For any other number b, if y = b^x then \log_b y = x