Quantities

When we use mathematics to model the physical world, we need additional tools to represent physical quantities. A number only gives a magnitude. When we combine that number with a unit (length, mass) it becomes a quantity that can represent something physical.

Dimensions, units, quantities

  • A quantity represents a physical measurement like mass, length or amount of energy
  • We represent a quantity with a number and a unit
  • The dimension of a quantity is different than the unit
  • For example 1 inch is the same as 2.54 centimeters even though 1 and 2.54 are not the same number

Physical Quantities

  • Our numbers are often helping us represent physical quantities
  • Examples:
    • The length of a tree
    • The number of animals observed
    • The number of molecules of mercury in a fish
  • A physical quantity is expressed as the product of a unit and a numerical factor

Dimensions

  • These physical quantities often have a dimension
  • Examples:
    • Length
    • Time
    • Mass

In our estimations, we may have quantities that are not in fundamental units such as length or time. For example, we may be counting a population of animals, or the number of power plants needed.

Units

  • To quantify dimensions, we use units
  • One dimension may have multiple units
  • Length: inches, miles, kilometers, light-years
  • Mass: grams, pounds, kilograms
  • There are also systems of units like SI or English

Measurement

  • Each measurement we make is an estimation of the physical quantity

Consequences

Adding and Subtracting

6 meters plus 170 pounds has no meaning since these are different dimensions.

You can add 5 feet and 3 meters if you convert to same unit first.

Multiplying and Dividing

5 feet multiplied by 10 pounds could have meaning even though these are different dimensions. (In this case if we have a 5 feet lever with 10 pounds of force at the end, that is 50 foot-pounds of torque.)

Multiplying with Quantities

  • Multiplying a length by a number gives a length
    • 1 meter times 10 equals 10 meters
    • 1 stride times 10 strides equals 10 strides
  • Multiplying a length by a length gives an area
    • 1 foot times 1 foot equals 1 square foot

Dividing with Quantities

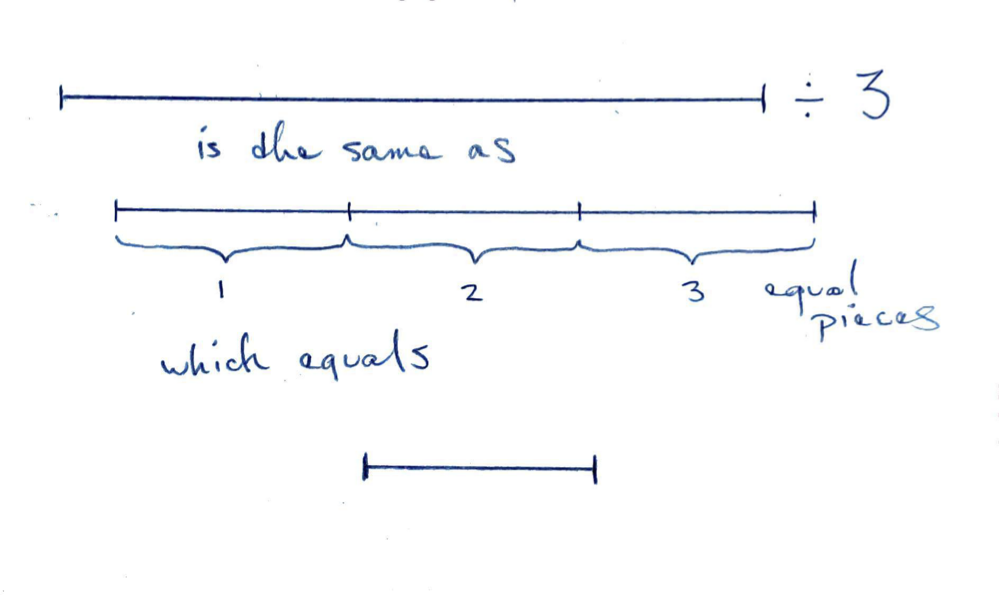
Divide length by number
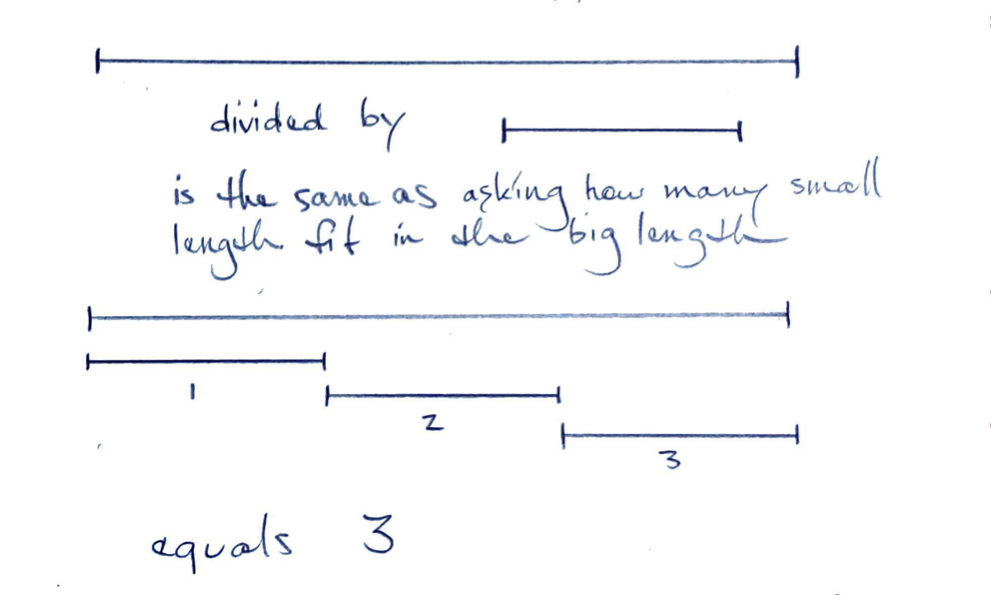
Divide length by length

Two units in the denominator

  • Births per capita per year
  • Hours per week per unit

Proportional Reasoning

  • You have a mass m of water and you see that when you add E joules of energy the temperature raises by T degrees. How much do you expect the water to raise if you add twice as much energy? Can you write this as a unit conversion?
  • You have a population of P people and they give birth to B babies over the course of a year. How many people do you expect them to give birth to over two years? How many births in a year do you expect if you have 2 million people?
  • It is widely assumed that students will spend 3 hours each week for every unit of credit they are taking in college. How many hours a week do you need to spend for a two unit class? How many hours do you need to spend over two weeks for a one-unit class?

Combinations of units

  • We often combine units to express new quantities

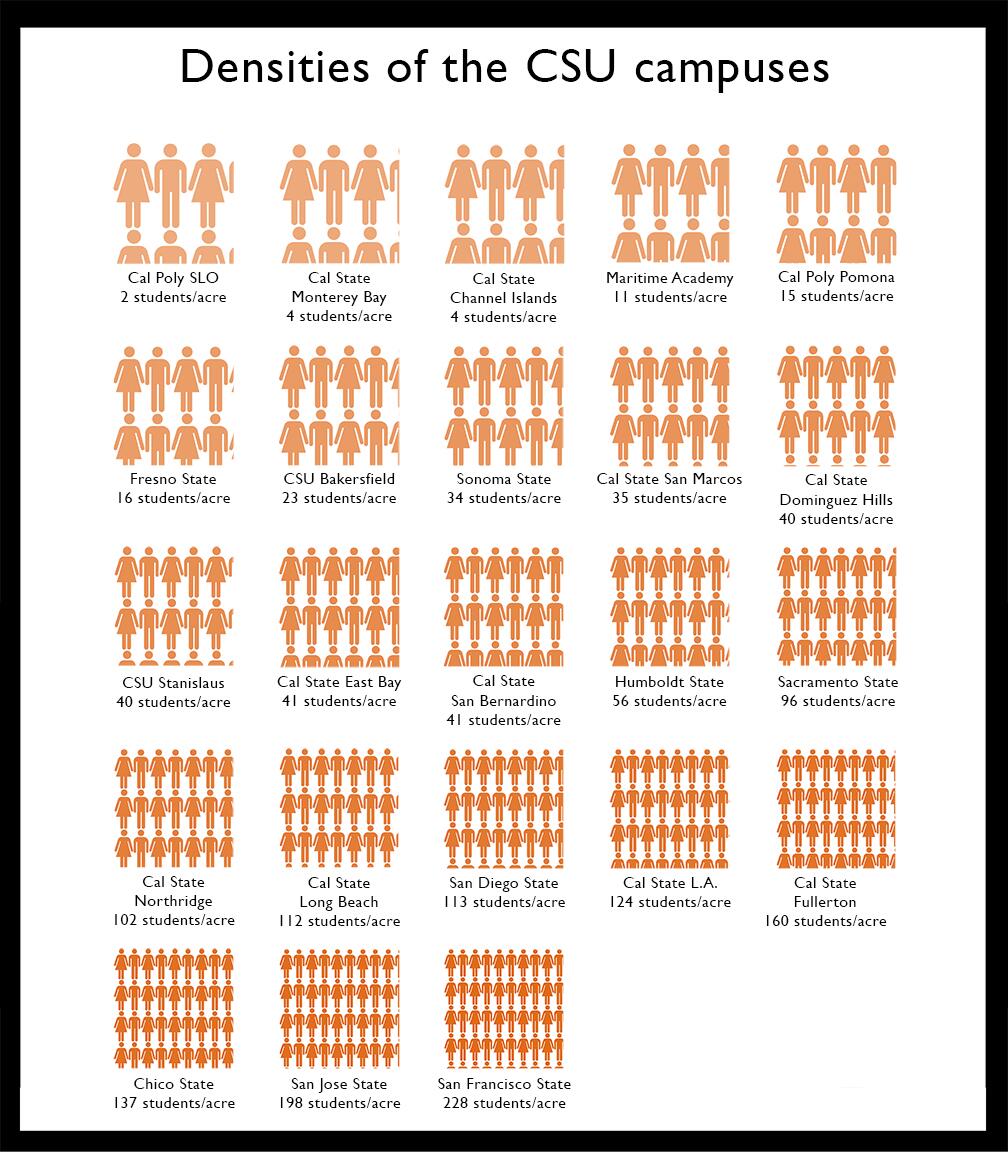
Student density

  • Students per acre
  • Number per area
  • Spans two orders of magnitude

Example: Units of students per acre

Cal State densities