Histograms and Distributions

So far, we have focused on single estimates. How much volume is this tank, how long is this room, etc. Now we ask questions about several objects at once.

  • How tall are the students in this class?
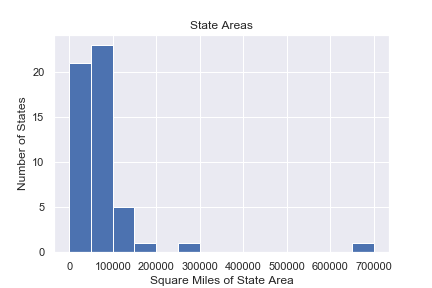
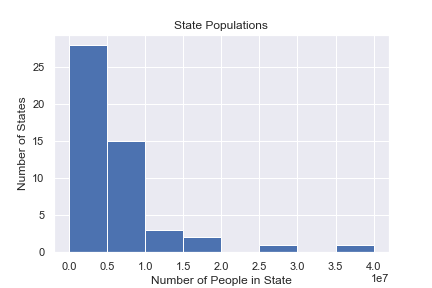
  • How big are the classes at my university?
  • How big are the departments at my university?

Here we are interested in the behavior of a single variable. Is it evenly distributed or are some values more present than others? What are the largest and smallest values?

Characterizing a body of data

We often ask two questions about data. The first is what is the central tendency or do the data point to some sort of majority value. The second is how tightly clustered are the data. Does the data range widely?

Mean or Average

A common measure of the central tendency is the mean. If we take a list of data, sum the values, and divide by the number of data we get the mean or the average.

Median

Another measure of the central tendency is the median. The median is the value at which half the data has a value below the median and half the data has a value above it.

Standard Deviation

The standard deviation is a measure of how dense or spare the data are around the central tendency.

Histogram

A common tool for looking at single-variable (univariate) data is a histogram.

A histogram

  • Shows data of a single quantitative continuous variable

  • Shows the value of that data on the x-axis

  • Divides the x-axis into evenly spaced bins

  • On the y-axis shows the number of values in each bin

  • We should know what values are being counted

State Areas

Here we show how to go from raw data to a histogram.

State Populations Alphabetical

With the data sorted we can see the median value as the one in the middle.

State Populations Sorted
State Populations Histogram

Normal Distribution

The normal distribution is a model that is a good approximation to a histogram of data. The real world doesn’t fit it exactly, but the model provides lots of practical power.

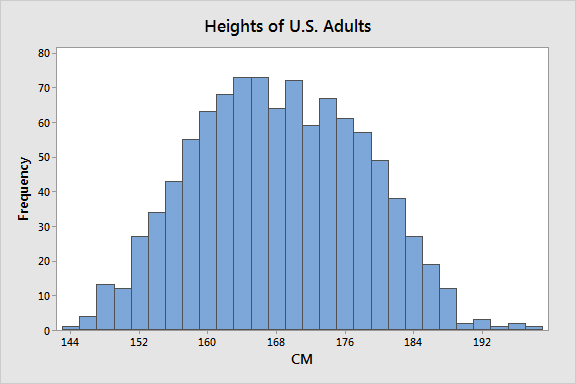
Many measurements and histograms are well-modeled by the normal distribution.

The x-axis is the value of a measurement and the y-axis is the relative frequency.

The area under the curve of a (normalized) probability distribution is exactly one.

The probability of a measurement occurring between two intervals is the area under the curve between those two intervals.

These probability distributions are models just like a rectangle or a circle. This probability distribution is usually a mathematical function.

For example, the gaussian distribution is given by

f = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/\sigma^2}

Notice our new friend, the number e, showing up.

Probabilities

These tools let you ask questions about how likely it is to observe events.

For example, if you pick a US adult at random, how likely are they to be 1.8 meters or taller?

Types of Data

  • Nominal data has no quantitative value.
    • Examples include state of birth, blood type, political affiliation
  • Ordinal data has a number and order but isn’t continuous
    • Example: survey question 1 for very unsatisfied, 5 for very satisfied
  • Continuous data: data that can take any value
    • Example: length, mass

Imposters

There are things that look like histograms but are not.

  • Time Series
  • Averaged Time Series
  • Bar charts with ordinal data