Logarithmic Scale

When you look at the vast majority of graphs and maps, moving a distance corresponds to adding a number. The ratio of distance to data does not change and this is called a linear scale.

With a logarithmic scale, moving a distance corresponds to a multiplication. Also, moving that distance corresponds to multiplying by the same number anywhere on the scale.

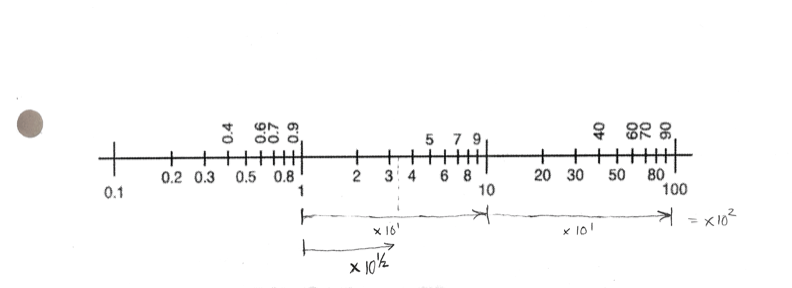
Here is an example of a logarithmic scale:

You can use a ruler or a marks on a piece of paper to convince yourself that the same distance results in the same multiplication or division.

Notice how this behavior of the logarithmic scale is different and similar to the behavior of a linear scale.

Logarithmic scale as a function

The logarithmic scale has some similarity to the linear scale.

Both scales are functions that map distance onto numbers. Both scales can be specified by a single number and a distance.

For the logarithmic scale, the distance represents multiplication by the number.

• multiplying a length by a number represents exponentiation
• dividing two lengths on a logarithmic scale represents logarithms

If l_c=4 cm represents multiplying by n=10, we can say:

f(l) = n^{\frac{l}{l_c}}

\log_n(f(l)) = \frac{l}{l_c}

Dividing by two lengths gives:

\frac{l_1}{l_2} = \frac{\log_n y_1}{\log_n{y_2}} = log_{y_2} y_1

Logarthmic scales create exponential graphs

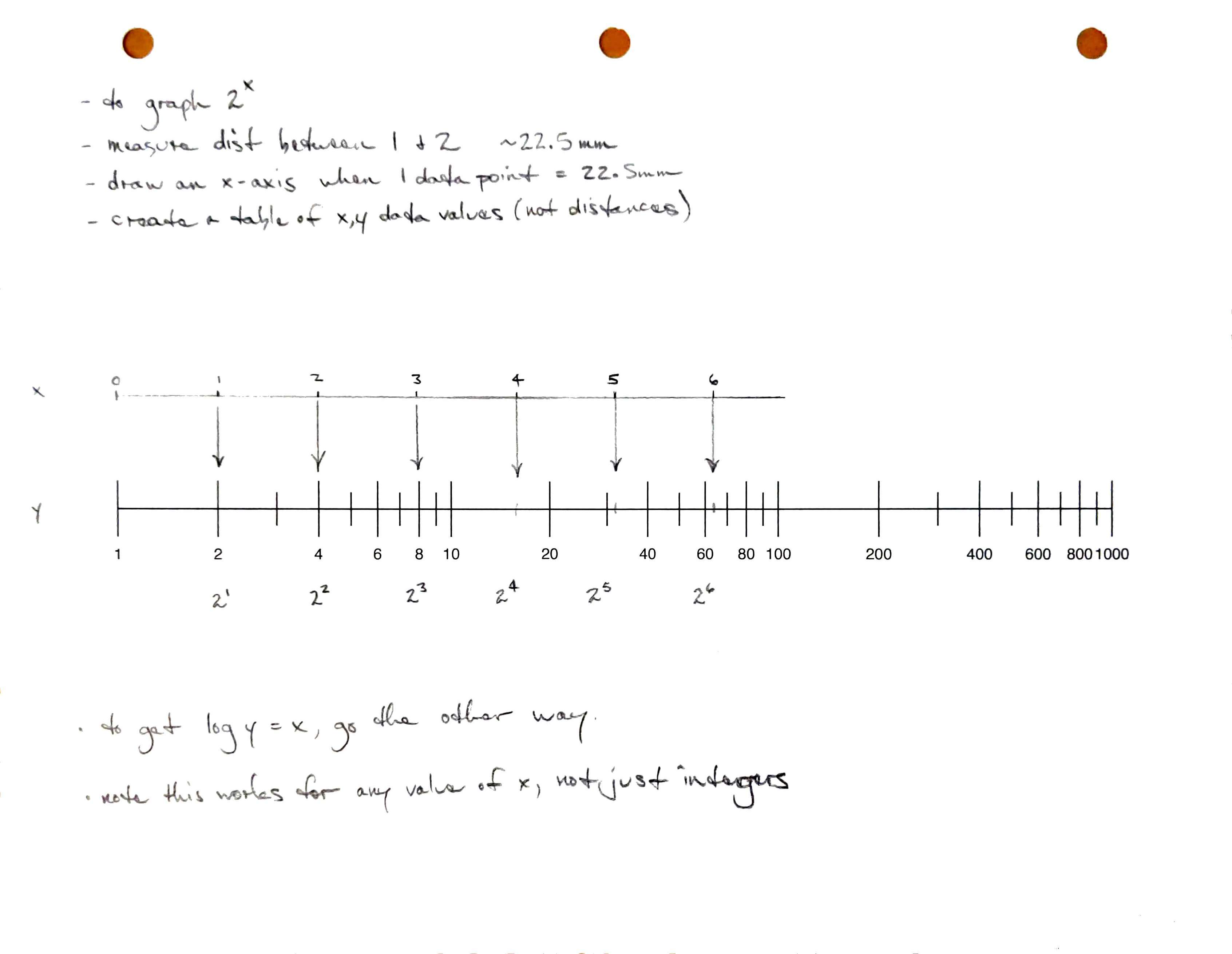
Exponential notation

You’ve probably seen notation like x^2 or x^3 several times before. In exponential notation, our symbol for a variable, x is in the exponent.

For example 2^x or 3^x.

Recall that 1 = 2^0, 2 = 2^1, 2 \cdot 2 = 2^2 = 4, etc. So, 2^x means to multiply 2 by itself x times.

Fractional Powers

Here we see that if we go a distance (about 50mm on the original paper drawing) we multiply by 10^1. Going twice that distance multiplies by 10^2. Going half that distance multilies by 10^{1/2}.

Relationship Between Exponents and Logarithms

The logarithm is the inverse of an exponential function.

That is if you know that

y = 10^x

then you can take the log of both sides to solve for x.

\log_{10} y = \log_{10} 10^x = x

Note that the logarithm function has to correspond to the number being exponentiated.

When we use the number e we use the natural log \ln

y = e^x

\ln y = \ln e^x = x

For any other number b, if y = b^x then \log_b y = x