We often want to determine where we stand in relation to a distribution. If we have an observation, is it typical or unusual for our distribution. What percentage of the data is above or below it?
We use areas to determine this.
Percentile
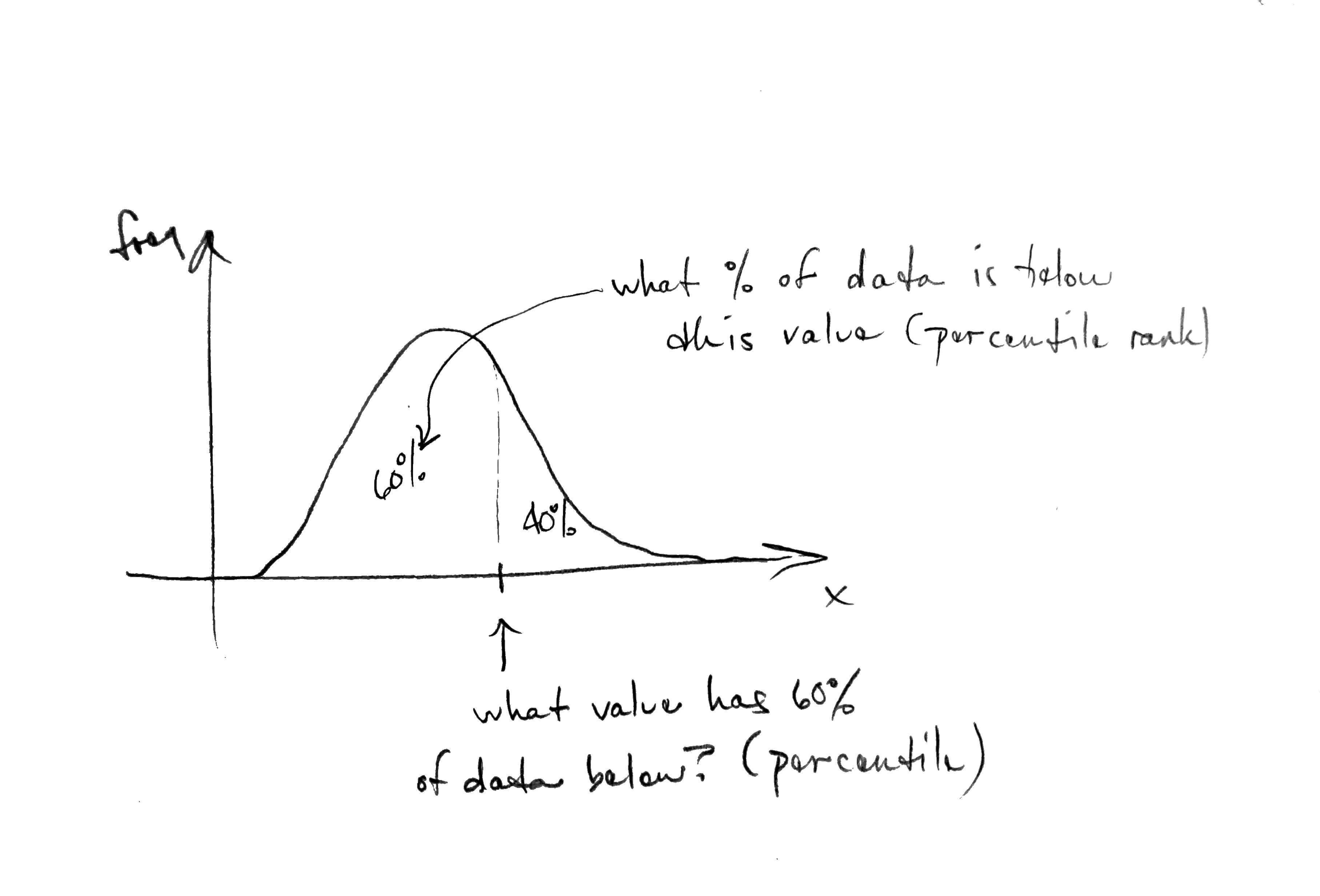
As we ask about the relative probabilities in a distribution, we use the percentile. The Xth percentile is the value Y at which X percent of the data has a value below Y. We interpret this as the area below a value on a probability distribution.
For example, the median is the same thing as the 50th percentile. That is, what is the value where 50% of the data is below that value.
This is useful for understanding the shape of a distribution. You may hear the terms quartiles, quintiles, or deciles which split the data into four, five, or ten equal sized groups.
The percentile will have units of the measurement of the group.
The 60th percentile of CalEnviroScreen asthma would be the asthma measurement for which 60% of the asthma measurements are below that value in the data set.
Relative probability
If you can calculate or estimate the area under the curve of a histogram or distribution, you can predict the probability of an event occurring.
For example, if we want to know the probability of a measurement between 1 and 2 occuring, we estimate the area under the curve between 1 and 2 and divide by the total area under the curve.
Percentile Rank
The percentile rank is the inverse of the percentile. It tells you the percentage of the data that has a value below the data Y.
This is useful for understanding if your observation is typical or unusual.
The percentile rank has no units since it is telling you the fraction of the data below your observation.
PR = \frac{\text{values below Y}}{\text{all values}}
You could input your income and figure out if you are in the 99% or the 1% using percent rank.
Computing metrics
We should be able to estimate these metrics by looking at a distribution and comparing areas. If we want precise values, we will use a computer.
Drawing a Histogram
- identify source of data
- identify what each data point will be
- find maximum and minimum of data
- decide on number of bins and bin ranges
- tally data points in each bin
- draw rectangles proportional to data points in each bin