Conduction
Fourier’s Law
The fundamental formula for heat conduction in a material is Fourier’s Law.
q = -k \nabla T
- q has dimensions of power per unit area
- k has dimensions of power per distance per degree
- T is the temperature over space
- \nabla computes the direction and magnitude of the greatest temperature change
If you don’t speak vector calculus (most don’t) the formula tells you that
- the direction of heat energy flow is in the direction of decreasing temperature
- the amount of heat energy flow is proportional to a material property, k, and how abrupt the temperature change is.
- the minus sign tells us heat flows from hot to cold
Consequences
If a material is very hot on one side and cool on the other, there will be a large amount of heat flow.
If a material has a uniform temperature, there is no heat flowing.
Conduction
Fourier’s law covers many complex situations, but we can simplify this for our purposes.
Our simplification is called one-dimensional, steady-state conduction and it works for many real-life applications including buildings.

If we have
- a material (the bar in the middle)
- negligible heat loss on the edges of material
- a steady warm temperature on one side
- a steady cool temperature on one side
- and have waited until the temperature is no longer changing
We can use the following formula:
q = \frac{k A \Delta T}{L}
Where q is the heat power flowing across the material, k is the conductivity, A is the cross-section area of the material, and \Delta T is the temperature difference on the sides of the material, and L is the length of the material in the same direction as the heat flow.
What this means is that if I know the properties of a building wall and the inside and outside temperature, I can predict how much power is flowing across it.
Fourier’s Law, Buildings Form
Walls and buildings have several elements (walls, sheetrock, insulation, lumber, etc.). We can combine these into a single value called the UA value to perform power estimations for an entire building.
q = U A \Delta T
- q heat transfer dimensions of power
- watts or BTU/hour
- U dimensions of power per area per
degree temperature
- watts/square meter/degree K
- BTU/hour/square foot/degree F
- A dimension of area
- square meters
- square feet
- T dimension of temperature
- Kelvin/Celsius
- Fahrenheit
| Quantity | Dimensions | Metric Units | Imperial Units |
|---|---|---|---|
| q heat transfer | power | watts | BTU / hour |
| U | power per area per temperature difference | watts / square meter / K | BTU / hour / square foot / F |
| R | area times temperature difference per power | square meter \cdot K / watt | square foot \cdot F \cdot hour / BTU |
| A | area | square meters | square feet |
| \Delta T | temperature difference | Kelvin or Celsius | Fahrenheit |
R-value
U = \frac{1}{R}
R has
- dimensions of area times temperature difference divided by power
- square meters times celsius per watt
- square feet times fahrenheit times hour per BTU
Formula and Unit Rodeo
The equation above is presented in several forms with different units.
q = UA \Delta T
q = \frac{1}{R} A \Delta T
Conductivity
This graph shows the range of conductivities for different materials.
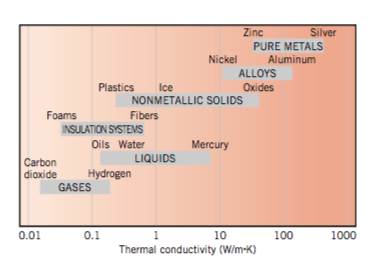
We can calculate the U-value of a material from
U = \frac{k}{L}
Examples
You have a wall with a UA value of 5 watts per Kelvin that is 25C on the surface of one side and 5C on the surface of the other side.
If the wall is at steady-state, how much heat is flowing in watts.
q = UA\Delta T q = 5 w/K \cdot (25C-5C) q = 100 W