To compare between competing proposals for energy, we often need to compare between money at different points in time. Even though the “amount” of money will be the same now and in the future, the value of that money changes over time. The mathematics of this section show how to convert between these.
Learning Objectives
- Calculate equivalent sums of money using discount rates
Equivalence principle
- Given a choice between money now and money later, most demand a larger value at a later date
- When someone is indifferent between sum 1 now and sum 2 at a fixed later date, the sums are considered equivalent
- This equivalence can be expressed using a discount rate
Equivalence principle as unit conversion
- You can think of using the discount rate as a unit conversion where you have units of dollars now and units of dollars in the future
- The equivalence in this case signifies the indifference of a consumer or an investor between the two values and points of time.
- However, our unit conversion is based on a more complicated model than a usual unit conversion.
Discount Formula
PV = \frac{FV}{(1+i)^n}
PV \cdot (1+i)^n = FV
\textrm{Present Value (USD)} = \frac {\textrm{Future Amount (USD)}} {(1 + \textrm{Discount Rate})^{\textrm{number of years in future}} }
This equation relates the present value PV and future value, FV. The present value is the future value divided by a factor containing the interest or discount rate (units of dollars per dollar per time period) and the number of time periods.
We can see that present values are less than future values. That is consumers require future values to be greater to be indifferent to the two options.
Unit Conversion Approach
You can think of dollars today (USD_0) and future dollars (USD_N) that are N years in the future as different units.
USD_0 = (1+i)^n \cdot USD_N
PV, the present value is the number of year zero dollars and FV is the number of year N dollars.
PV\ USD_0 \cdot \frac{(1+i)^N\ USD_N}{USD_0} = FV\ USD_N
Present Value Notation
Single payment PV = \frac{C}{(1+i)^n}
Stream of payments
Often an energy investment looks like the diagram below. We might make a large initial investment and then get benefits over several years of time. We then can sum these up into a single present or future value.
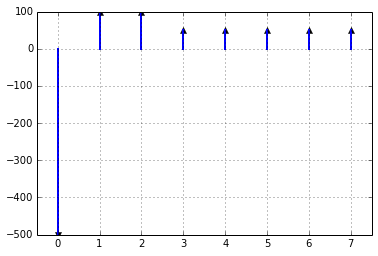
PV = C_0 + \frac{C_1}{1+i} + \frac{C_2}{(1+i)^2} + \cdots + \frac{C_N}{(1+i)^N}
Compact notation PV = \sum_{n=0}^{N} \frac{C_n}{(1+i)^n}
Discount rate vs. Interest rate
- Discount rate usually refers to personal preferences
- Interest rate is usually a real rate charged by a bank
Mathematical Model
In both the case of a discount rate and an interest rate, we use an exponential model. Our inflation calculations that assume a constant inflation rate also use an exponential model.
There is some controversy over the use of this discount rate model in climate change discussions.
David Roberts has an entertaining article on this topic.
Ideal Bank
As we’ve seen in electricity, ideal models are useful for analyzing problems.
We can consider an ideal bank which has
- same rate for deposits and loans
- no transaction costs
Internal Rate of Return
- Tells us at what interest rate a cash flow has a net present value of zero
- We will look at this on a spreadsheet
- This doesn’t have a closed-form solution
- Usually solved by a computer
Finding the IRR is the equivalent of asking, here is a loan and payments, what was the interest rate you got?
Inflation
Inflation
- The cost of goods usually rises over time
- This rate is monitored by the Consumer Price Index
- As prices rise, the value of money decreases
Inflation
1 + r_0 = \frac{1+r}{1+f}
- r_0 is the effective rate of interest
- r is the nominal rate of interest
- f is the inflation rate
For small inflation rates,
r_0 \approx r - f
NPV Spreadsheet Example
- Excel considers first value in the NPV function to be year 1
Examples
Indifference
You have a choice between receiving $10K now or a different amount five years in the future. If your discount rate is 10%, what is the future amount that you would perceive as equivalent.
PV = \frac{FV}{(1+i)^n} \$10K = \frac{FV}{(1 + 0.1)^5} FV = \$ 16.1K