Radiation
Radiation is the transfer of thermal energy by electromagnetic radiation.
Emission
Thermal energy (vibrations) in an object converts to a photon emitted from the surface.
The object is cooled since the photon carries away energy from the object.
Absorption
When a photon travels strike an object and its energy is converted to thermal energy.
The object is warmed by this additional energy.
Reflection
When a photon strikes the surface of an object and “bounces” away from the object.
Transmission
When a photon strikes the surface of object and continues traveling through the object.
Energy Balance
The radiant power absorbed, reflected, and transmitted are all equal at a given wavelength as these are the only three possibilities.
Emissivity
Different objects at the same temperature will emit different amounts of radiation per area depending on the emissivity of the surface.
If we have two objects with the same surface area and temperature, the object with the higher emissivity emits more radiation.
Emissivity varies between 0 and 1. Note that emissivity can vary by wavelength.
Black Body Model
A black body is an idealized object that absorbs all the radiation that hits it. We say that this has an emissivity of 1.
The emissivity is how much radiant power is emitted by a substance relative to an ideal black-body emitter where the emissivity is equal to 1.
We sometimes use a grey-body model where the emissivity at all wavelengths is equal but between one and zero.
Emissivity, Absorptivity, and Reflectivity
Kirchoff’s Law of thermal radiation states that a body in thermodynamic equilibrium, the absorptivity and emissivity are equal.
So materials with high emissivity at a wavelength are also strong absorbers and weak reflectors at that wavelength. Black paint is a good example.
Materials with low emissivity at a wavelength are weak absorbers and strong reflectors. Polished metal is a good example.
Spectral Dependence
- Radiation from the sun is around 0.5 um in wavelength.
- Radiation from room temperature objects is around 10 um in wavelength.
Radiant Heating
Many heating technologies use warm air to create heating by convection.
Radiant heating creates a warm surface with steam, hot water, or electrical heating and that warm surface radiates heat.
The hydronic floors in the Tuscany dorm use this technology.
Radiative Cooler
If a surface is able to reflect solar radiation (low emissivity for visible electromagnetic radiation) and radiate thermal energy (high emissivity at infrared wavelengths) it can reach a temperature lower than the air temperature.
Concepts
- Electromagnetic spectrum
- Emissivity
- Absorptivity
- Spectral response
- Planck Distribution
- Planck Law
- Net Radiative heat transfer
Radiation
- Why do you think radiant heat is important?
- Where do you observe radiant heat?
- What wavelengths are involved?
Thermal radiation
- What wavelengths do we refer to with thermal radiation?
- Why?
Using Thermal Radiation
- If we want something to absorb thermal radiation, what properties are necessary?
- If we want something to shed thermal radiation?
- What if we want to use sunlight to warm something?
- What if we want light but not heat?
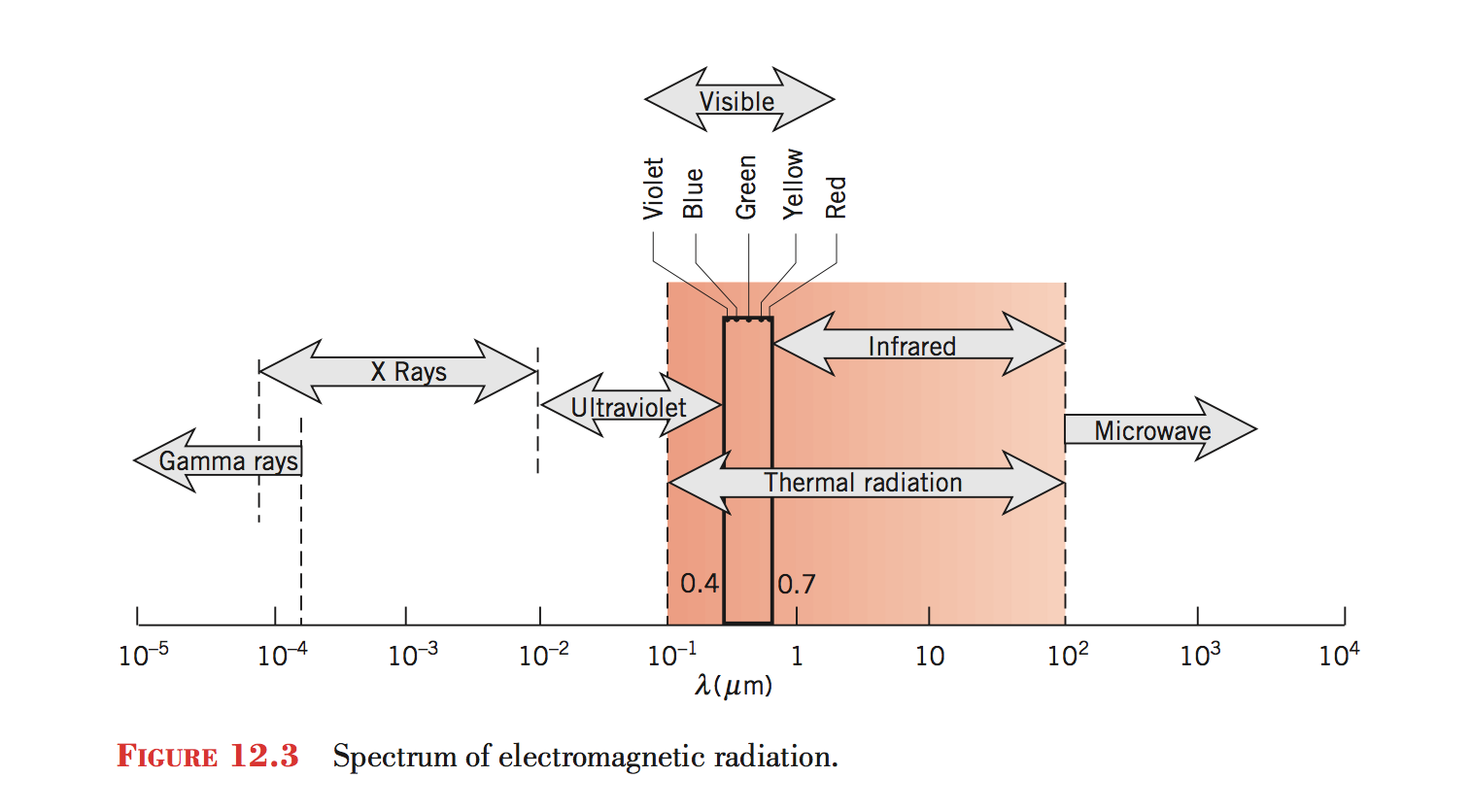
Spectrum
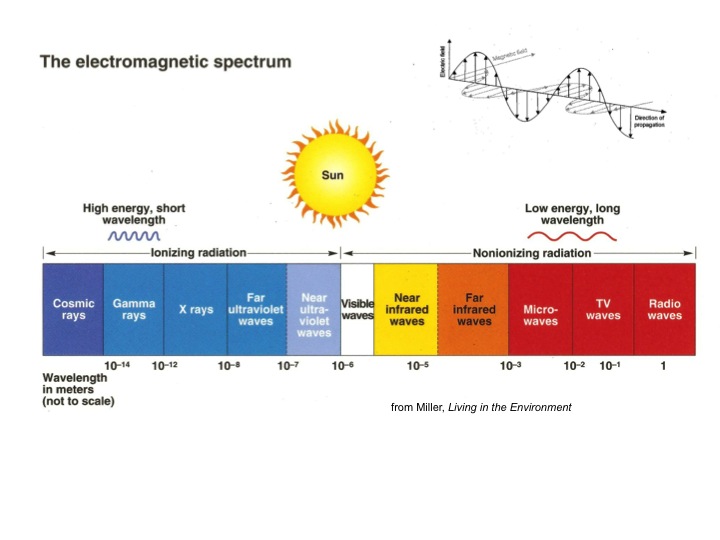
Spectrum
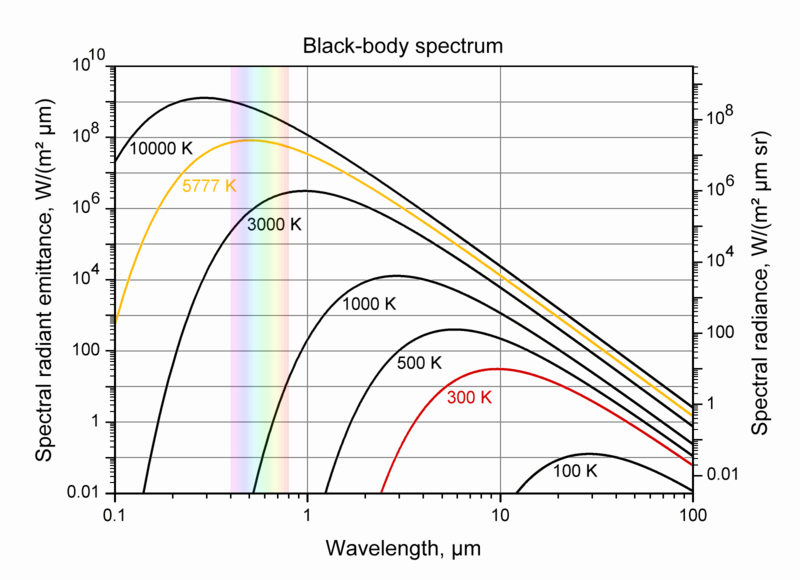
Blackbody Spectrum
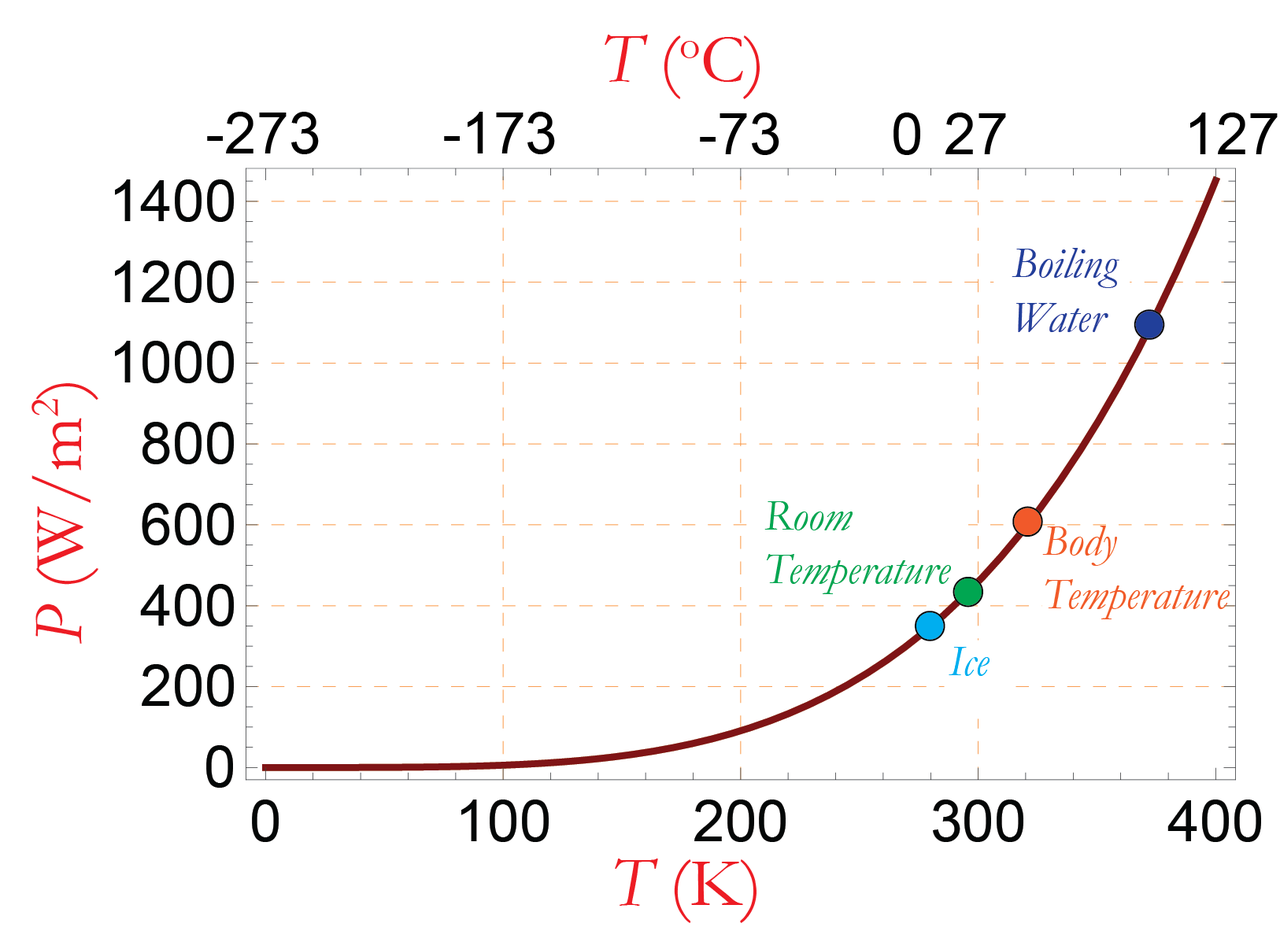
Blackbody radiation
- What does the spectrum of radiation look like for the sun?
- Which part of this is thermal?
- What does the spectrum of radiation look like for the earth?
- Which part of this is thermal?
Planck’s law
- How do the wavelengths emitted changes as a substance increases in temperature?
Planck’s law
This law relates the intensity of power at each wavelength with the temperature of an object (ideal black-body).
B_\lambda(\lambda, T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm{B}T}} - 1}
Stefan-Boltzmann law
- What predicts the total radiant power from a hot object?
Stefan-Boltzmann law
This law relates the total power emitted to the temperature, surface area, and emissivity of an object.
P = A \epsilon \sigma T^4
| A | surface area | square meters |
| \epsilon | emissivity | dimensionless |
| \sigma | Stefan-Boltzmann constant | 5.67\cdot 10^{-8} W per square meter per K^4 |
| T | temperature | Kelvin |
Emissive Power
Emissivities

Radiation Power
An object with surface area A and emissivity P at a temperature T emits power according to this equation:
P = \epsilon \sigma A T^4
Where \sigma is the Stefan-Boltzmann constant, 5.67 \cdot 10^{-8} watt per square meter per Kelvin^4.
Net Radiative Heat Transfer
Objects are usually surrounded by other radiating objects and are absorbing radiation from those objects. So, we use the following formula where T_1 is the temperature of the radiating object and T_2 is the temperature of the surroundings.
P = \epsilon \sigma A (T_1^4 - T_2^4)
Radiation transfer between surfaces
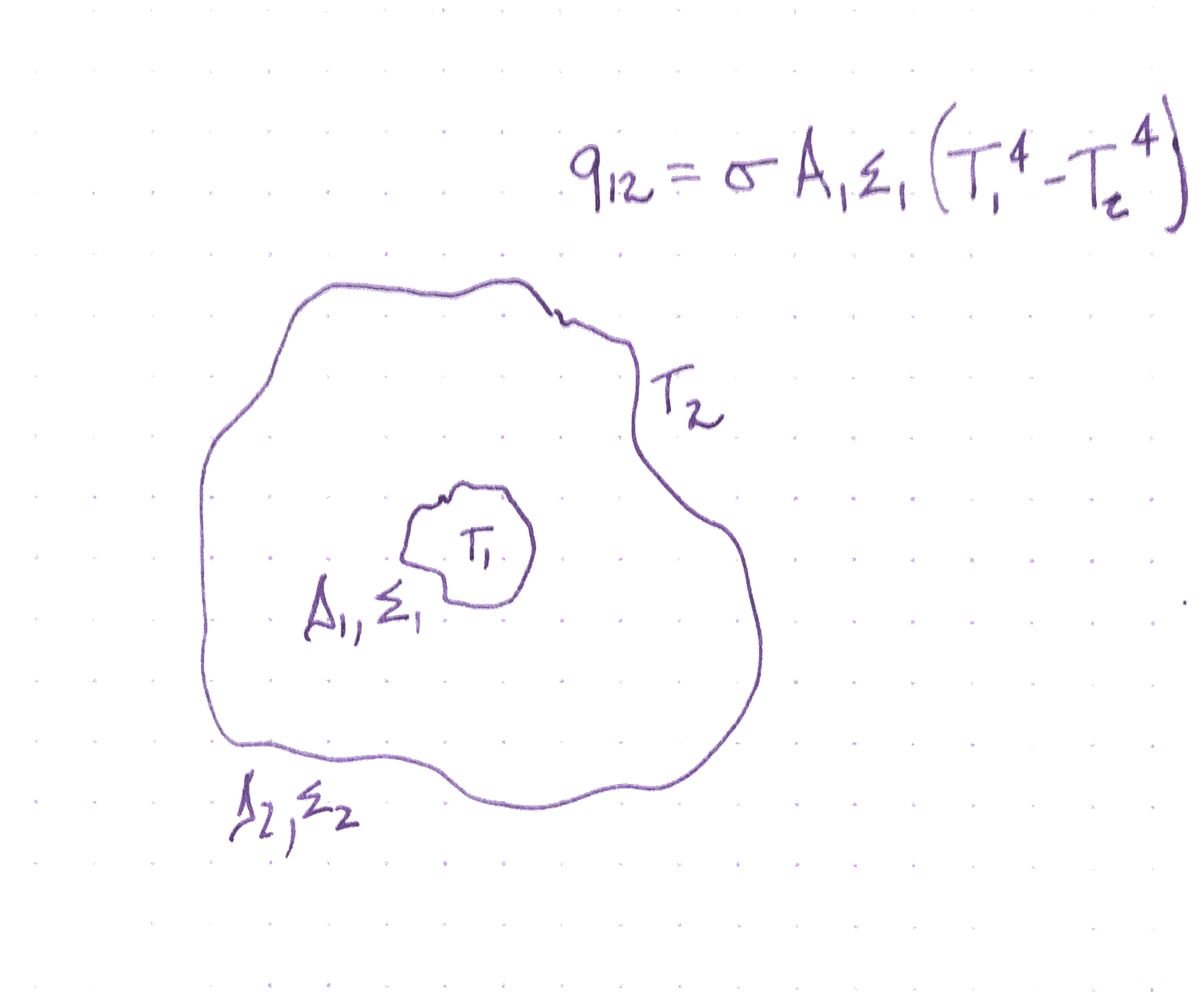
Radiation transfer between surfaces
- Why is it colder on clear nights?
Demonstrations
- What do you expect when you view an IR image of a glass incandescent light bulb?
- Do you expect to read the same temperature from a reflection of a hot object as a direct view of the hot object? Does the material matter?