How much solar energy strikes a collector?
Solar energy strikes the earth, passes through the atmosphere, and strikes the collector panel at an angle.
We can create a prediction by
- Calculate extraterrestrial insolation
- Correct the attenuation by the air mass
- Correct for the angle between the collector and the sun’s rays
Theory vs Practice
- I’ll demonstrate mathematical expressions for solar radiation
- In practice you will use tables or software applications that calculate these values
Radiation units
- Power per unit area (watts per square meter) (W/m^2)
- Power = Power per unit area \times area
- Energy = Power \times Time
- Insolation is usually reported in power or energy per area.
Extraterrestrial solar radiation
- This is the sunlight striking the top of the atmosphere
I_0 = SC \left( 1 + 0.034 \cos\left(360n/365)\right)\right)
Where SC = 1367 W/m^2 and is called the solar constant.
Note the relatively small effect of the time of year.
Air mass ratio

Air mass ratio
- There are some standard air mass ratios we use
- AM0 is “in space”
- AM1 is for noon-day sun
- AM1.5 is the standard test condition that resembles year round insolation
Atmospheric absorption
- Air mass ratio
- I_B = Ae^{-km}
- I_B - insolation at earth’s surface (W/m^2)
- A - insolation in space (W/m^2)
- k - optical depth (no units)
- m - air mass ratio (no units)
Note that this is exponential decay.
We now have, I_B, the radiation at the earth’s surface.
Angle of the sun and panel
- I_{BC} = I_B \cos \theta
- I_B - insolation at earth’s surface (W/m^2)
- I_{BC} - insolation on collector (W/m^2)
- \theta - no units
- \cos \theta - no units
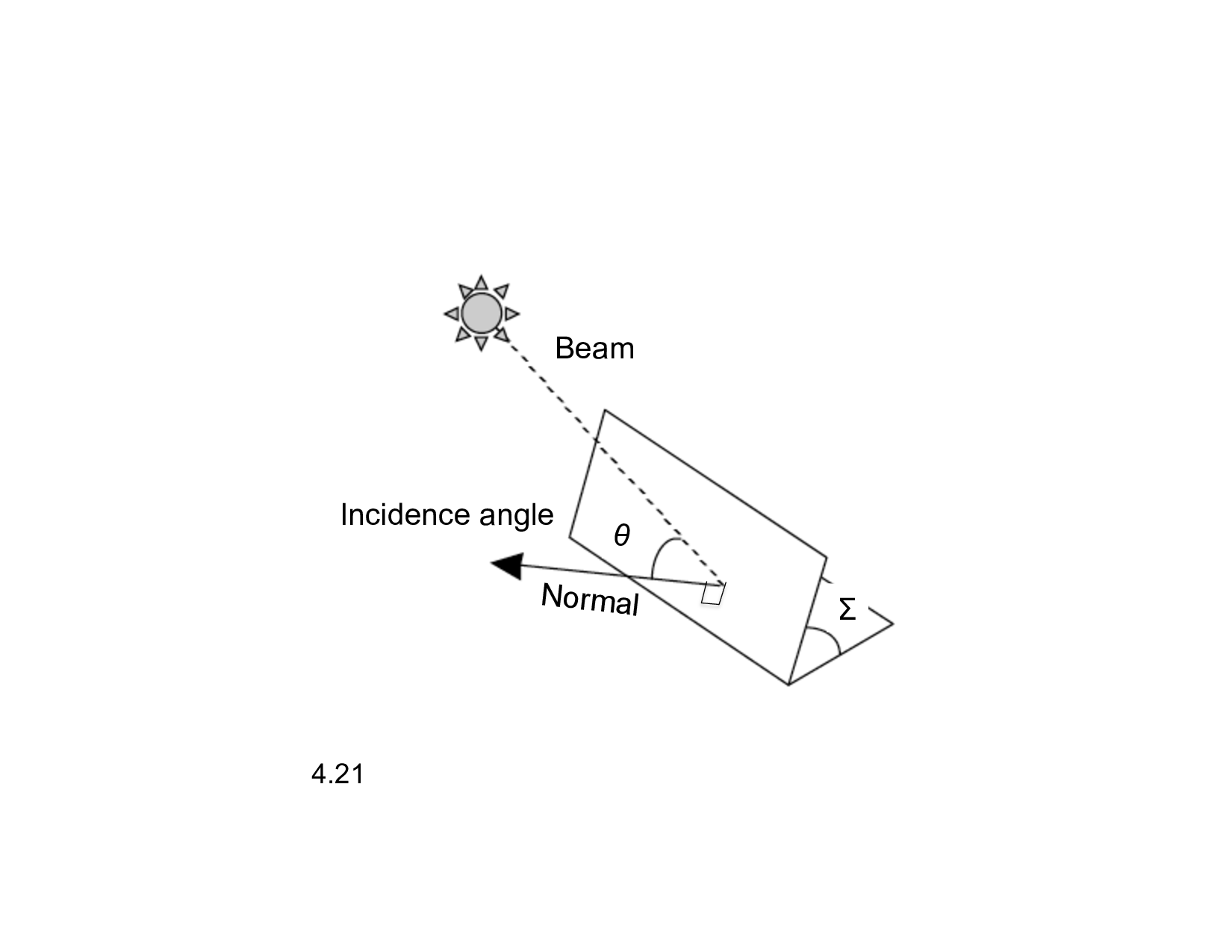
Determining the angle between rays and panel
- We can directly measure
- We can predict from time of year, day, and panel orientation
Normal angle
- The normal is a vector perpendicular to a plane
- The angle between this normal and the sun’s rays determines the collected radiation
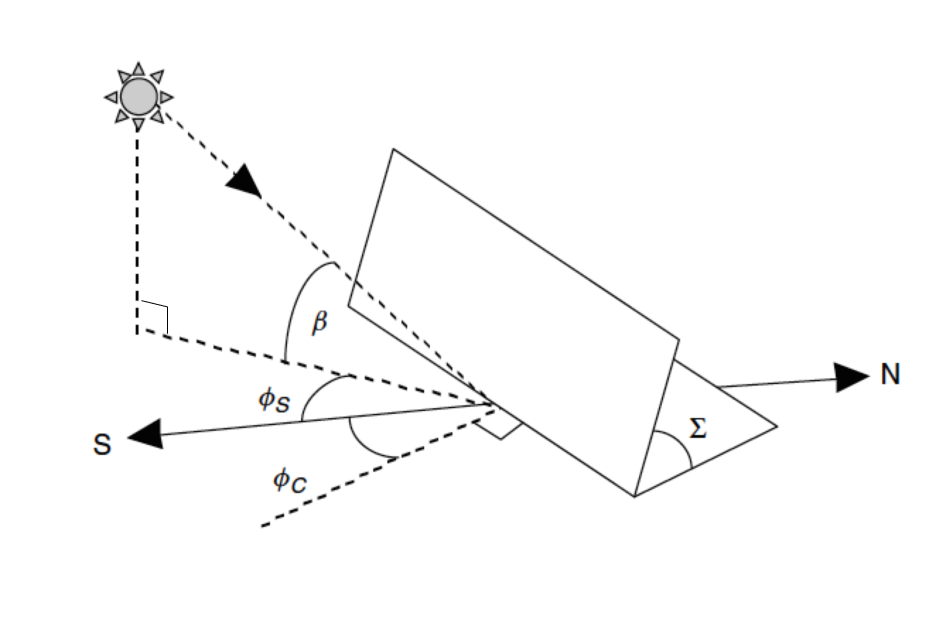
Angle between sun and panel
\cos\theta = \cos\beta\cos(\phi_s - \phi_c)\sin\Sigma + \sin\beta\cos\Sigma
- \theta - angle between direct beam and panel normal
- \beta - solar elevation
- \phi_s - solar azimuth angle
- \phi_c - panel azimuth angle
- \Sigma - panel tilt
Angle of the sun and panel
We can determine the angle of the sunlight and the panel from the sun’s elevation and azimuth, and the tilt and angle of the panel.
Common panel tilt
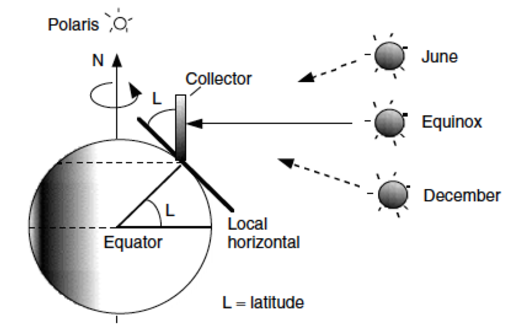
Panels tilted at the latitude so equinox sun strikes directly.