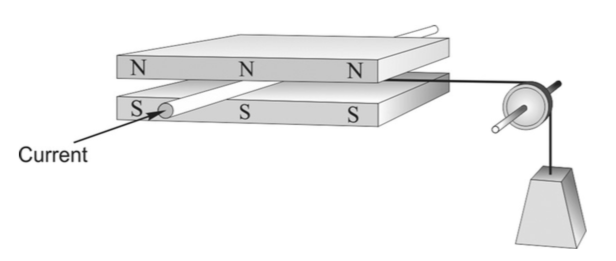
Motor principles

  • A current carrying coil of wire creates a magnetic field
  • This magnetic field exerts a torque on a magnetic field

Simple DC Motor Model

This simple model allows us to predict the behavior of many motor types.

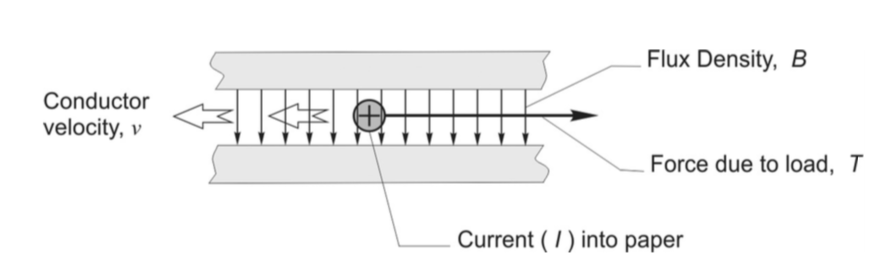
Torque and Current

Torque is equal to the field times the current times the length of wire.

T = BIl

Voltage and Angular Velocity

The induced voltage or back-emf, is equal to the field times the length of wire times the velocity of the wire.

E = Blv

Motor Constants, Torque, and Speed

The torque is proportional to the current through the motor.

T = k I

In this equation, I is in amperes and k is in newton meters per amp.

The induced back EMF is proportional to the speed of the motor.

E = k \omega

In this equation, \omega is in radians per volt and k is in volt seconds per radian.

If we use RPM instead of radians per second, we use this equation:

E = RPM / Kv

where Kv is in RPM per volt.

Heating Loss

The electrical input power equals the mechanical output power plus the copper loss or heating (I^2R).

Power, Torque, and Angular Velocity

The mechanical output energy is equal to the torque times the angle over which that torque was applied.

E = \tau \theta

This is analogous to work equals force multiplied by distance.

P = \tau \omega

Power equals torque multiplied by the angular velocity.

Voltage Constant

  • Often called Kv and expressed in rpm/volt
  • We can convert this to radians per second per volt

\frac{rev}{min}\frac{1}{volt}\frac{2\pi\ rad}{rev}\frac{min}{60 sec} = \frac{rad}{volt \cdot sec}

Torque Constant

Note that the torque constant is the reciprocal of the voltage constant when the voltage constant is in radians per volt per second.

\frac{rad}{volt \cdot sec} = \frac{rad \cdot coulomb}{joule \cdot sec} = \frac{amp}{newton \cdot meter}

Electrical Power

The electrical power is the current times the voltage.

Notice that part of the electrical energy is converted to heat in the resistor. Our model has the rest of the energy converted to mechanical energy in the motor.

Example

You have a motor with an motor constant, Kv of 8.5 rpm/volt. The motor has an internal resistance of 1 ohm. (This is equivalent to 1.12 N-m/amp.) You want your motor to spin at 60 rpm while providing 10 N-m of torque.

  • What should your applied voltage V be?

Note that this is essentially a voltage divider question, so we use the same strategies but the physical conditions of the motor tell us about the induced voltage and the current flowing through the motor.

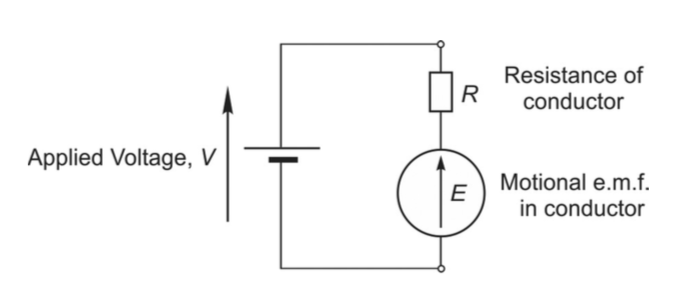
Here is the circuit of the motor connected to the voltage source.

Here is the equivalent circuit for the motor.

The voltage to operate the motor is the sum of the induced (back EMF) voltage, E, and the voltage across the resistor. We find E from the rpm and the motor constant. We find the voltage across the resistor from the current which we find from the torque.

E = 60 rpm \cdot \frac{volt}{8.5\ rpm} = 7.1 V I = 10 Nm \cdot \frac{amp}{1.12 Nm} = 8.9 A

We use this current to find the voltage drop on the resistor.

V = IR = 8.9 A \cdot 1 \Omega = 8.9 V

The necessary voltage is then 8.9V + 7.1V = 16V.

To find the efficiency, we divide the mechanical power by the power delivered by the voltage source. The power delivered to the motor is P = IV = 16V \cdot 8.9A = 142W

In the resistor we lose P = I^2R = (8.9A)^2 \cdot 1 \Omega = 79 W

The mechanical power is the torque times the angular velocity.

P = \tau \omega = 10 Nm \frac{60\ rev}{min} \frac{2\pi\ rad}{rev} \frac{min}{60\ sec} = 63 W

So 142 total watts delivered by the voltage source equals 63 W mechanical power plus 79 watts of heat in the coils.

\eta = \frac{63\ W\ mech}{142\ W\ input} = 0.44

Further Investigation